題名：人生はπ^2と関係があるのだ　-仮説自由択-
報告者：ダレナン

　本報告書は、基本的にNo.983の続きであることを、ここで前もってことわりたい。

　先の報告書にて、「人生はドーナツなのだ」という一つの提言を行った。ここでは、さらにそれを拡張すべく、自由(あるいは、テキトー)な仮説の選択、言い換えると、仮説自由択として、人生に関する循環を提言したい。まさしく、これを、再度天才バカボン風に言えば、「人生はπ2と関係があるのだ　-仮説自由択-」となる。とりあえず、天才バカボン的に、とある仮説を”建築”していると見做していただければ幸いである。
　スリンキーの連続体として人生を問うと、大きな輪と小さな輪(スプリングの個々の輪)の循環から、次の図が提示できる。点線は大きな輪に相当し、実線は小さな輪に相当する。すると、各々の輪の円周は、

2πr

で求められる。ここで、rは半径である。そして、大きな輪も小さな輪も、「トポロジーの世界では、ブスと美人を差別せず、博愛主義なのです。もっと正確にいえば、ブスとか美人とかに価値観をもたないのです。」1)との条件を満たす変幻自在性を帯びることから、両輪とも直径が1（半径rは1/2）とでき、そのことから、大きな輪も小さな輪もともに円周が

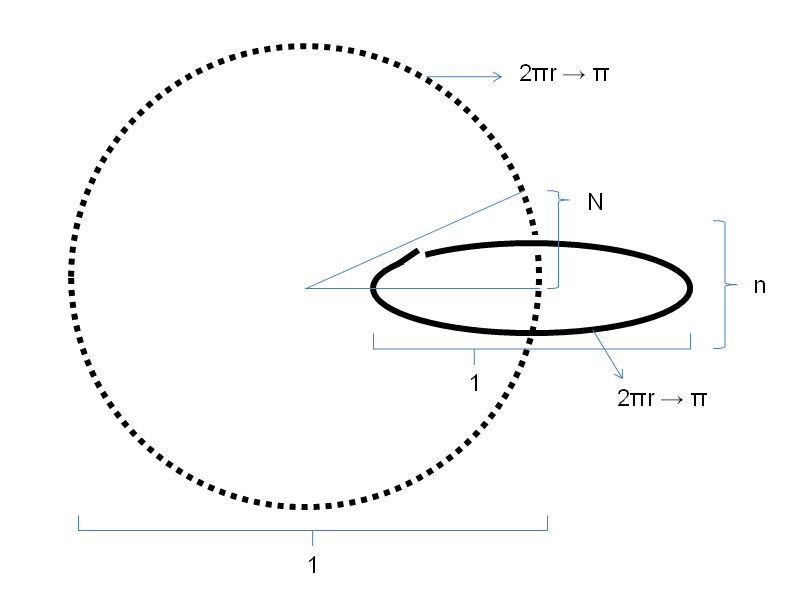
図　スリンキーの連続体の概念図

π

となる。そして、スリンキーの連続体の小さな輪の循環(年単位で繰り返すイベント)がn、大きな輪の循環がN(生から死までの年)で示されるとすると、厚みや幅のないトーラスΣ1(ドーナツ)の人生的な循環の区切りは、

π/N nπ→ n/N π^2

で収束する、とできる。ここで筆者と同じく天才数学者レオンハルト・オイラー博士を傾愛してやまない方であれば、ふと、気づくであろうか。そう、「平方数の逆数の無限和の値は」というバーゼル問題、式で表すと、次のように書かれる問題である。

1/1^2 +1/2^2 +1/3^2 +1/4^2 +⋯=

この式の右辺は、

π^2/6

となる。
　ここで、偉大なレオンハルト・オイラー博士の、偉大なる解法が、人生の循環へと繋がる瞬間である。

1) 川久保勝夫: トポロジーの発想 ○と△を同じと見ると何が見えるか. 講談社. 1995.

…「トポロジーの発想 ○と△を同じと見ると何が見えるか」の品への案内は、こちらになります。


地底たる謎の研究室のサイトでも、テキスト版をご確認いただけます。ここをクリックすると記事の題名でサイト内を容易に検索できます。